ScienceDirect - Computers & Operations Research : A tabu search algorithm for the routing and capacity assignment problem in computer networks

Jian Shen ^,^,^a, Fuyong Xu^a and Peng Zheng^b

^a School of Information Science and Engineering, Lanzhou University, Lanzhou 730000, PR China
^b Department of Electrical and Computer Engineering, University of California, Irvine, CA 92697, USA

Available online 9 June 2004.

1. Introduction

Network design is a fundamental problem with a large scope of applications that have given rise to many different models and solution approaches [1 and 2]. The general network design problem involves the minimization of a cost objective function over a lot of design variables, such as link capacities, flow assignment, network topology, node locations, message priority discipline. The joint problem of routing and capacity assignment, also known as the capacity and flow assignment (CFA) problem, is a special issue of the general network design problem.

The CFA problem was first considered by Gerla in his thesis [3]. Fratta et al. [4] proposed a model to minimize mean network delay in the case of general bifurcated routing and linear design costs, allowing the application of the flow deviation algorithm to solve the corresponding convex multicommodity flow problem. Ng and Hoang [5] examined a special case of the routing and capacity assignment problem in which a m-M/M/1 queuing structure is used to model parallel transmission lines. They formulated the problem using continuous link capacity variables, and used the flow deviation method for solution. LeBlanc and Simmons [6] formulated the routing and capacity assignment problem using continuous link capacity variables and suggested a new convex delay function different from the traditional M/M/1. Gavish and Neuman [7] proposed a model to jointly minimize the delay and capacity costs in the case of nonbifurcated routing and discrete capacity functions. The model was solved using a Lagrangean relaxation procedure. Gavish and Altinkemer [8] extended the work in [7] by considering all possible routes for every communicating node pair. They included cut constraints that are redundant in the original problem to improve the lower bounds and proposed an interesting heuristic to generate a feasible solution. Amiri and Pirkul [9] developed a new mixed integer nonlinear programming formulation for the CFA problem using Lagrangean relaxation and subgradient optimization techniques and a two phases heuristic solution procedure to obtain lower bounds as well as feasible solutions. The model overcame the shortcoming of previous methods. The results were compared to those reported in [8]. Amiri [10] presented a new mathematical programming model that includes a constraint that sets an upper limit on the average link queuing delay in the network, and considered all possible routes for every communicating node pair. Amiri and Pirkul [11] developed the model in [10] with multi-busy-hour traffic conditions. Mahey et al. [12] considered discrete capacities and the cost function combines the installation cost with a measure of the quality of service (Qos) of the resulting network for a given traffic, and proposed a mixed integer nonlinear model of the joint capacity and flow assignment problem solved by a generalized Benders decomposition method. Queiroz and Jr. [13] proposed a heuristic method for the continuous capacity and flow assignment problem by rephrasing the problem in the context of concave programming and bringing an alternative formulation of the projected pairwise multicommodity flow polyhedron. The key idea is to use local minima to define concavity cuts, thus avoiding cycling and an explicit enumeration of the vertices.

Several authors incorporated reliability constraints into the CFA problem. Monma and Sheng [14] presented a global network design and analysis model to analyze network performance in low-cost backbone packet-switched networks. Lim [15] proposed an optimal procedure for minimizing the total link cost of the common channel signaling network under joint performance and reliability constraints. Al-Rumaih et al. [16] proposed a methodology for network topology design considering the problems of single link and node failures tolerances. Their method is based on systematic topological modifications of an initial network constructed without reliability requirements but for which the link capacities satisfy a set of link and path performance requirements. Chamberland and Sanso [17] presented a model to take failures into account in the CFA problem. The model provides a way to evaluate a trade-off between increasing capacity and lower performance in the event of failures. Two different algorithms, corresponding to two different levels of parallelism, were proposed and implemented.

The previous methods, however, are all traditional mathematical programming techniques with high complex computation process. The results generated by these methods are local optimal solutions instead of global optimal ones.

In recent years, a new tabu search (TS) metaheuristic algorithm has been quickly developed. It was introduced by Glover [18, 19 and 20], and successfully applied to solve the problems, such as graph coloring [21], traveling salesman problem [22], flow shop sequencing [23], job shop scheduling [24], and many other combinatorial optimization problems [25 and 26]. In the area of telecommunications, Laguna and Glover [27] discussed the development of a TS method for the bandwidth packing problem. Costamagna et al. [28] presented a TS algorithm for topological optimization of broadband communication networks. Chamberland and Sanso [29] presented a tabu search algorithm for topological expansion of multiple-ring metropolitan area networks. Berger et al. [30] applied a TS for a network loading problem with multiple facilities. Shyur and Wen [31] developed a simple TS for optimizing the system of virtual paths in an ATM network. Youngho et al. [32] developed an effective TS procedure to provide tight upper bounds for a fiber routing problem arising from the design of optical transport networks.

The achieved success of TS in all applications is due to its implementation as problem-oriented. For each implementation, it needs particular definitions of structural elements and parameters. In order to study the performance of TS, a simple TS algorithm for the classical CFA problem is proposed in this paper. The performances of the algorithm are compared with the traditional techniques, and extensive tests are made to determine appropriate parameter values for the TS algorithm.

The remainder of the paper is organized as follows. In Section 2, the CFA problem is formulated. Section 3 describes the TS algorithm for the CFA problem. The results of computational experiments are presented in Section 4. Finally we conclude and suggest further research in Section 5.

2. Problem formulation

The classical routing and capacity assignment problem can be described as follows: given a basic topology and a requirement matrix, how to simultaneously select link capacities and routes used by nodes in the network in order to ensure an acceptable performance level at a minimum cost [7, 8 and 9]. This problem is a complex nonlinear programming which has many restrained conditions and it is known to be NP-completeness [33, 34, 35 and 36].

In order to formulate the classical CFA problem, we make the same assumptions used in [7, 8 and 9]. It is assumed that the network topology, the queuing and capacity cost structure, and the traffic requirements between every pair of communicating nodes are given. We also assume that nodes have infinite buffers to store messages waiting for transmission on the links, that the arrival process of message to the network follows a Poisson distribution and that message lengths follow an exponential distribution. We further assume that the propagation delay in the links is negligible, that there is no message processing delay at the nodes, and there is only a single class of service for each communicating node pair. Under these assumptions, the computer network is modeled as a network of independent M/M/1 queue [37 and 38] in which links are treated as servers with service rates proportional to the link capacities. The customers are messages whose waiting areas are the network nodes.

We use the following notation:

The objective function is to minimize the total cost of network given by expression in Eq. (1). The first term of the objective function indicates the total cost of delay. The second term refers to the total fixed cost computed as the sum of the initial setup cost and the distance cost. The third term is the variable cost associated with the links in the network. The constraint (2) guarantees the feasibility of the flow on each link in terms of the capacity assigned to it. The constraints ((3) and (4)) guarantee that only one route for each origin-destination pair and only one line type is chosen for each link, respectively.

3. Tabu search for the CFA

Tabu search is a procedure using ideas from artificial intelligence, which guides local search methods to overcome local optimality and obtain optimal or near optimal solutions for hard combinatorial optimization problems. Starting from an initial solution, the method explores the solution space by moving from a solution to the best solution in the neighborhood at each iteration. This allows the method to escape from a local optimum and explore other regions of the search space, but the quality of the solution may deteriorate from one iteration to the next, which distinct TS form the classical local search methods. To avoid cycling, a specially designed memory mechanism, known as the tabu list, is used to store previously visited solutions or certain attributes of them, which will not be reversed for a certain number of iterations. In particular, the status of a tabu move can be overruled and make accessible right away if a certain aspiration criterion is met. For a more comprehensive description of TS, readers can refer to [25].

Since the TS is compared with the traditional techniques in this paper, we propose a simple TS algorithm for the CFA problem, and the fundamental components of the procedure are specified in the following.

3.1. Solution representation

To a communicating origin-destination node pair p,p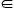Π, there are |S_p| candidate routes, among which one and only one is selected to route the corresponding traffic. Using an integral variable r_p to represent the index number of the route, we will get |Π| such variables all together, each representing a certain route for a node pair. A route vector r=(r₀,r₁,Λ,r_|Π|−1) can be obtained if we put all the |Π| variables together, for 0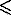r_p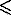|S_p|−1. To a link l,l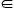L, there are |I_l| candidate capacity types, among which only one is assigned to a line. Using an integral variable c_l to represent the index number of the capacity types. We will get |L| such variable all together, each representing a capacity type for a line. A capacity vector c=(c₀,c₁,Λc_|L|−1) can be obtained if we put all the |L| variables together, for 0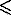c_l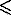|I_l|−1. It is natural for us to use these two vectors to represent a solution of the CFA.

3.2. Initial solution

Usually there are advantages to starting from an initial solution that is of high quality. We study the following methods for the CFA problem.

3.2.1. Initial route selection

We use four route methods as follows:

The random route method (RRM): Each time before the TS procedure starts, a program is used to generate |Π| random integers, which lie in the interval [0,|S_p|−1]. Let components of the route vector r equal those random numerals respectively, so an initial route solution could be attained.

The shortest route method (SRM): For each communicating node pair, select the shortest route from its candidate route set to carry the corresponding traffic.

The minimum hops method (MHM): The hop of a route is defined as the number of nodes (or links) it traverses. This method is to select the one with the minimum hops from the candidate route set for each communicating node pair.

The longest route method (LRM): For each communicating node pair, select the longest route from its candidate route set to carry the corresponding traffic.

3.2.2. Initial capacity assignment

Many methods can also be applied to the capacity assignment. In this paper, we only adopt the best capacity assignment method. If the routes of all communicating node pairs have been selected, the flow of each link is also decided. In the candidate capacity set, there must be a best candidate capacity value that can make the total cost of network is the minimum. We can find these capacity values, and assign to the links.

3.3. Move definition

Two kinds of moves are defined only to route solution, i.e., M₊ and M₋. The former can lead to a tentative solution r_t=r_c+e_i, and the latter, r_t=r_c−e_i. For e_i is an identical vector and r_t and r_c represent the trial solution and the current solution, respectively. Obviously, those two moves satisfy the ‘completeness’ condition, i.e., any solution, wherever it lies in the solution space, can be reached from another solution through certain number of such moves.

3.4. Tabu list

A list (Fig. 1) is used to form the tabu list. Each unit in the list consists of two parts, i.e., the index number of the communicating node pair, which ranges from 0 to |Π|−1, and the operations imposed on it, which is represented by either 0 or 1, where 0 refers to M₊ and 1 to M₋. For example, a unit containing (10,0) means that the move is prohibited if it leads to r_t=r_c+e₁₀. The tabu list operates as first-in-first-out (FIFO) stacks. During the search procedure, a new tabu move is added at the end of the list and the oldest move is removed from the head of the list.

Fig. 1. The structure of tabu list.

The length of the list is tabu list size (T_max). The tabu list size represents the number of iterations that a move remains tabu, preventing the search from cycling. When the tabu list is short, tabu moves are allow to be reversed after few iterations, which makes the search emphasize intensification. If the tabu list is long, many moves are tabu and the search is forced into areas that were not yet visited, which makes the search focus on diversification. Thus the size of the tabu list should depend on the size and the characteristics of the problem suggested by Glover [25]. In the experiments, we investigate various values of the tabu list sizes.

3.5. Neighborhood search strategy

The neighborhood search strategy specifies which move in the neighborhood is chosen at each iteration. It is of great importance for the solution quality and the search efficiency. The following three methods are tested.

The best method (BM): Generate and evaluate all solutions in the neighborhood of the current solution. Choose the move yielding the solution with the best objection function value as the next move. Note that if the move is tabu, the best non-tabu move is selected.

The first method (FM): Generate sequentially the set of solutions in the neighborhood of the current solution. Choose the first move identified as yielding a solution with the improved objective function value. If no improving move exists, select the best non-tabu move.

The sample method (SM): Under the conditions where the neighborhood size is very large, it is time-consuming to search the whole neighborhood. The sample method randomly generates a neighborhood subset of the current solution. All solutions in this subset are obtained and evaluated, and the move yielding the best objective function value is chosen as the next move. If the move is tabu, the best non-tabu move in the subset is selected.

3.6. Aspiration criterion

Compared with the constraining effect of tabu restrictions, aspiration criteria make the search process free. An aspiration criterion is designed to overrule tabu status and make a candidate move in tabu status admissible. In this article, the following aspiration criterion is used: if a move gives a better objective function value than the best found so far, then it can be taken as the next move in spite of its tabu status.

3.7. Stopping criterion

Many stopping criteria can be developed depending on the nature of the problem being studied. The most common criterion, which is employed in this paper, is a maximum number of iterations.

3.8. Objective function

The objective function of the CFA problem is given in Eq. (1). However, in many cases, it is difficult to seek a feasible solution or it will take considerable time to seek such one, which satisfies the constraints mentioned above. So we redefine the objective function for the CFA problem as follows:

where, C is a large, positive constant, which is 1×10⁵ in this paper. By doing so, we can transfer the constrained optimization problem into an equivalent non-constrained problem, which is convenient in practice.

3.9. Tabu search procedure

Based on the previous discussion, we present a TS procedure for the CFA problem.

Step 1. Initialization: Generate an initial solution (r₀,c₀) according to the selected initial method, and calculate the total cost Z(r₀,c₀); Initialize the current solution (r_c,c_c) and the best solution (r_b,c_b) by setting (r_c=r₀, c_c=c₀) and (r_b=r₀, c_b=r₀), respectively; initialize the tuning parameters.
Step 2. Neighborhood search (SM): (1) Generate a neighborhood subset M, and all solutions in M are obtained. (2) Evaluate solutions: Let (r_tb,c_tb) be the best solution for Z(r_tb,c_tb) is minimum in M. If the move (r_c→r_tb) is not tabu, and Z(r_tb,c_tb)<Z(r_b,c_b), go to (3); otherwise go to (4). If the move is tabu, but corresponding Z passes the aspiration criterion, i.e. Z(r_tb,c_tb)<Z(r_b,c_b), go to (3); otherwise let (r_tb,c_tb) be the solution for Z(r_tb,c_tb) is the nearest minimum in M, repeat this step. (3) Renew the best solution: Set (r_b=r_tb, c_b=c_tb) and Z(r_b,c_b)=Z(r_tb,c_tb). (4) Move: Set (r_c=r_tb, c_c=c_tb). (5) Modify the tabu list: Put the opposite move into the tabu list and remove the oldest move in it.
Step 3. Check stopping criterion: If the stopping criterion is satisfied, go to step 4; otherwise go to step 2.
Step 4. Stop and report the results.

4. Computational results

We studied the four topologies shown in Fig. 2, Fig. 3, Fig. 4 and Fig. 5, viz. ARPA, OCT, USA and RING. These networks along with traffic parameters and cost structure are similar to those tested in [7, 8 and 9]. In all four networks each node communicates with every other node. In the ARPA network there were 420 communicating node pairs with 4 messages per second being sent along the chosen route. The corresponding values were 650 and 1 for OCT, and 650 and 4 for USA, and 992 and 1 for RING. The set of candidate routes was obtained using a modified shortest path algorithm previously, and 5 routes were chosen for every communicating node pair. The different capacities used in the base case and their corresponding cost components are presented in Table 1. The algorithm was coded in C language and run on a PC with Pentium III-866 MHz CPU.

Fig. 2. The topology of ARPA network.

Fig. 3. The topology of OCT network.

Fig. 4. The topology of USA network.

Fig. 5. The topology of RING network.

Table 1. Link capacity set and its cost components

Table 2 shows the results with different message lengths. In order to compare the effectiveness of our procedure with the traditional method, we also report the results obtained by Amiri and Pirkul [9]. The unit cost of delay is assumed to be $2000 per month per message for the base case. Both fixed and variable cost multipliers are equal to 1. Computational results indicate that both delay cost and overall cost decrease compared with the results in [9]. The lower delay cost, the shorter response time to users. That is to say, our proposed TS algorithm obtained the minimum total cost and the better quality of service at the same time. We also noticed that the solutions are slightly improved in ARPA network. With the increasing of the network scale, the results have a significant improvement. In OCT network the total cost reduced 67%. In USA network it is 59%, and 61% in RING. It can be concluded from these results that TS is effective in solving the CFA problem, and superior in large scale networks.

Table 2. Computational results with different message lengths

In order to implement the proposed algorithm effectively, the properties of the key tabu parameters are examined.

Fig. 6 shows the results with different methods used to generate the initial solution. It can be seen that the initial solution has a significant effect on the results. The solutions of SRM and MHM are superior to those of RRM and LRM. There is slight difference between SRM and MHM. This can be attributed to the fact that MHM is used to select the route with the minimum hops or links, as a result, the overall traffic in each link is lighter, and the total cost is lower compared with other methods. Because in most cases, fewer hops means shorter distance and vice versa, the difference between MHM and SRM is negligible. The results indicate that the good initial solution should be selected to improve the quality of solutions while using TS. For the CFA problem, the initial solution should be generated by MHM or SRM, which is used for the rest of the study.

Fig. 6. Results with different initial solution methods (RING).

Fig. 7 and Fig. 8 show the effects and the CPU times with different neighborhood search strategies. We observe that the neighborhood search strategy make a significant impact on the performance of TS procedures, particularly when the neighborhood size is large. BM, in most cases, can yield better solutions, but with most computation time. The solutions obtained by SM are very close to those by BM, with lest CPU times. FM spends less CPU times than BM, but it leads to worse results in each case, making it unsuitable for the TS procedure. Considering the solution quality and efficiency at the same time, we can draw a conclusion that SM should be selected with higher priority when using TS. Only in circumstances where the size of neighborhood is small or time is not so critical, can BM be applied.

Fig. 7. Results with different neighborhood search strategies (RING).

Fig. 8. CPU times with different neighborhood search strategies (RING).

When SM is used, how to select the neighborhood sample size is another important problem. The results with different neighborhood sample sizes are given in Fig. 9. Obviously, if the sample size is too small, the algorithm could not find a good solution. When the sample size is equal to 50 (about 5% of the whole neighborhood), the algorithm arrives in an optimal solution. With the increase of the size, the solutions have a slight improvement but pay more computational efforts. Therefore, 5% of the neighborhood should be selected as a subset in practice.

Fig. 9. Results with different neighborhood sample sizes (RING).

The results and the CPU times with different tabu list sizes are reported in Fig. 10 and Fig. 11, respectively. It is observed that the tabu list with a size of 7 that proposed by Glover [25] is also suitable for the CFA problem. When the tabu list size is small (<7), the algorithm visits the same sequence of solutions over and over again, and ends up in a local optimum. When it is large (>7), the results have slight improvement with the increase of the tabu list size, but at the expense of more computation time. So it is reasonable to select 7 as the tabu list size for the CFA problem.

Fig. 10. Results with different tabu list sizes (RING).

Fig. 11. CPU times with different tabu list sizes (RING).

In addition, the average number of iterations and the average CPU time for both our method and the method proposed by Amiri and Pirkul [9] are summarized in Table 3. Evidently, our TS algorithm is able to converge very quickly to an optimal solution. The optimal solution could be found at the average iteration 90, which is approximately 3 times less than the method in [9]. It is need to point out that the solution method described in [9] was written in Pascal and run on IBM-3081D. Taking machine differences into account, our method is still faster than the traditional techniques. These further illustrate the high efficiency of the TS method.

Table 3. Average number of iterations and CPU times

5. Conclusions

In this paper, a tabu search metaheuristic algorithm is proposed for the classical CFA problem in computer networks. Better results are obtained compared with the traditional techniques, so the high effectiveness of the TS method is further verified. Extensive computational experiments show that appropriate parameters will greatly improve the effectiveness and efficiency of the TS procedure. These results are also helpful to the other sophisticated performance optimization problems in computer networks.

In future research work, the performance of the TS method will be further studied. Advanced intensification and diversification strategies [39], and parallel, reactive and hybrid TS methods [40, 41 and 42] should be applied to improve the quality of the solutions. In addition, we will apply the TS method to some new optimization problems arising in computer networks, for instance, the weight setting problem in OSPF routing [43], etc.

References

1. M. Minoux, Network synthesis and optimum network design problems: models, solution methods and applications. Networks 19 (1989), pp. 313–360. Abstract-INSPEC | $Order Document | MathSciNet

2. V. Ahuja. Design and analysis of computer communication networks, McGraw-Hill, New York (1982).

3. Gerla M. The design of store-and-forward networks for computer communications. Ph.D. thesis, University of California, Los Angeles, 1973.

4. L. Fratta, M. Gerla and L. Kleinrock, The flow deviation method: an approach to store-and-forward communications network design. Networks 3 (1973), pp. 97–133. Abstract-Compendex | $Order Document | MathSciNet

5. T. Ng and D. Hoang, Joint optimization of capacity and flow assignment in a packet-switched communications network. IEEE Transactions on Communications 35 2 (1987), pp. 202–209. Abstract-Compendex | Abstract-INSPEC | $Order Document

6. L. LeBlanc and R. Simmons, Continuous models for capacity design of large packet-switched telecommunication networks. ORSA Journal on Computing 1 (1989), pp. 271–286. Abstract-INSPEC | $Order Document

7. B. Gavish and I. Neuman, A system for routing and capacity assignment in computer communication networks. IEEE Transactions on Communications 37 4 (1989), pp. 360–366. Abstract-Compendex | Abstract-INSPEC | $Order Document | Full Text via CrossRef

8. B. Gavish and K. Altinkemer, Backbone network design tools with economic tradeoffs. ORSA Journal on Computing 2 (1990), pp. 226–252.

9. A. Amiri and H. Pirkul, Routing and capacity assignment in backbone communication networks. Computers & Operations Research 24 3 (1997), pp. 275–287. Abstract | Full Text + Links | PDF (955 K)

10. A. Amiri, A system for the design of packet-switched communication networks with economic tradeoffs. Computer Communications 21 (1998), pp. 1670–1678.

11. A. Amiri and H. Pirkul, Routing and capacity assignment in backbone communication networks under time varying traffic conditions. European Journal of Operational Research 117 (1999), pp. 15–29. Abstract | Full Text + Links | PDF (222 K)

12. P. Mahey, A. Benchakroun and F. Boyer, Capacity and flow assignment of data networks by generalized Benders decomposition. Journal of Global Optimization 20 (2001), pp. 173–193. MathSciNet

13. Queiroz M, Jr. CH. A heuristic for the continuous capacity and flow assignment. European Journal of Operational Research 2003;146:444–59.

14. C. Monma and D. Sheng, Backbone network design and performance analysis: a methodology for packet switching networks. IEEE Journal on Selected Areas in Communications 4 6 (1986), pp. 946–965. Abstract-INSPEC | Abstract-Compendex | $Order Document | Full Text via CrossRef

15. Y. Lim, Minimum-cost dimensioning model for common channel signaling networks under joint performance and reliability constraints. IEEE Journal on Selected Areas in Communications 8 9 (1990), pp. 1658–1666. Abstract-Compendex | Abstract-INSPEC | $Order Document | Full Text via CrossRef

16. A. Al-Rumaih, R. Ahmed, S. Bakry and A. Al-Dhelaan, A methodology for network topology design with link and node failures tolerance. International Journal of Network Management 6 1 (1995), pp. 42–64.

17. S. Chamberland and B. Sanso, Sequential and parallel approaches to incorporate reliability in the synthesis of computer networks. Journal of Network and Systems Management 5 2 (1997), pp. 131–157. Abstract-Compendex | Abstract-INSPEC | $Order Document | Full Text via CrossRef

18. F. Glover, Future paths for integer programming and links to artificial intelligence. Computers & Operations Research 19 (1986), pp. 533–549. Abstract | Full Text + Links | PDF (2265 K) | MathSciNet

19. F. Glover, Tabu search-part I. ORSA Journal on Computing 1 3 (1989), pp. 190–206. Abstract-INSPEC | $Order Document

20. F. Glover, Tabu search-part II. ORSA Journal on Computing 2 1 (1990), pp. 4–32. Abstract-INSPEC | $Order Document

21. A. Hertz and D. Werra, Using tabu search techniques for graph coloring. Computing 39 (1987), pp. 345–351. Abstract-INSPEC | Abstract-Compendex | $Order Document | MathSciNet

22. M. Malck, M. Guruswamy and M. Pandya, Serial and parallel simulated annealing and tabu search algorithms for the traveling salesman problem. Annals of Operations Research 21 (1989), pp. 59–84.

23. J. Barnses and M. Laguna, Solving the multiple-machine weighted flow time problem using tabu search. IIE Transactions 25 (1993), pp. 121–128.

24. M. Dell'Amico and M. Trubian, Applying tabu search to the job-shop scheduling problem. Annals of Operations Research 41 (1993), pp. 231–252. Abstract-INSPEC | $Order Document | Full Text via CrossRef

25. F. Glover and M. Laguna. Tabu search, Kluwer Academic Publishers, Dordrecht (1997).

26. I.H. Osman and G. Laporte, Metaheuristics: a bibliography.Annals of Operations Research 63 (1996), pp. 513–623. Abstract-INSPEC | $Order Document

27. M. Laguna and F. Glover, Bandwidth packing: a tabu search approach. Management Science 39 4 (1993), pp. 492–500. Abstract-INSPEC | Abstract-Compendex | $Order Document

28. E. Costamagna, A. Fanni and G. Giacinto, A tabu search algorithm for the optimization of telecommunication networks. European Journal of Operational Research 106 2–3 (1998), pp. 357–372. Abstract | Full Text + Links | PDF (1617 K)

29. S. Chamberland and B. Sanso, Topological expansion of multiple-ring metropolitan area networks. Networks 36 4 (2000), pp. 210–224. Abstract-INSPEC | $Order Document

30. D. Berger, B. Gendron et al., Tabu search for a network loading problem with multiple facilities. Journal of Heuristics 6 (2000), pp. 253–267. Abstract-INSPEC | Abstract-Compendex | $Order Document | Full Text via CrossRef

31. C.C. Shyur and U.P. Wen, Optimizing the system of virtual paths by tabu search. European Journal of Operational Research 129 (2001), pp. 650–662. SummaryPlus | Full Text + Links | PDF (247 K) | MathSciNet

32. L. Youngho, H. Junghee and K. Kugchang, A fiber routing problem in designing optical transport networks with wavelength division multiplexed systems. Photonic Network Communications 5 3 (2003), pp. 247–257.

33. B. Gavish and S.L. Hantler, An algorithm for optimal route selection in SNA networks. IEEE Transactions on Communications 31 10 (1983), pp. 1154–1161. Abstract-Compendex | $Order Document | Full Text via CrossRef

34. S. Narasimhan, H. Pirkul and P. De, Route selection in backbone data communication networks. Computer Networks and ISDN Systems 15 (1988), pp. 121–133. Abstract | Full Text + Links | PDF (961 K)

35. B. Gavish and H. Pirkul, Efficient algorithms for solving multiconstraint zero-one knapsack problems to optimality. Mathematical Programming 31 (1985), pp. 78–105. Abstract-Compendex | Abstract-INSPEC | $Order Document | MathSciNet

36. M.R. Garey and D.S. Johnson. Computers and intractability : a guide to the theory of NP-completeness, Freeman, San Francisco (1979).

37. L. Kleinrock. Communication nets : stochastic message flow and delay, Dover, New York (1964).

38. Kleinrock L. Queueing systems, vols. 1–2. New York : Wiley-Interscience; 1975–1976.

39. M. Dell'Amico, A. Lodi and F. Maffioli, Solution of the cumulative assignment problem with a well-structured tabu search method. Journal of Heuristics 5 (1999), pp. 123–143. Abstract-Compendex | Abstract-INSPEC | $Order Document | Full Text via CrossRef

40. R. Battiti and G. Tecchiolli, The reactive tabu search. ORSA Journal on Computing 6 2 (1994), pp. 126–140. Abstract-INSPEC | $Order Document

41. T.G. Crainic and M. Gendreau, Cooperative parallel tabu search for capacitated network design. Journal of Heuristics 8 (2002), pp. 601–627. Abstract-INSPEC | Abstract-Compendex | $Order Document | Full Text via CrossRef

42. T. Trafalis and S. Kasap, A novel metaheuristics approach for continuous global optimization. Journal of Global Optimization 23 (2002), pp. 171–190. Full Text via CrossRef

43. M. Ericsson, M.G.C. Resende and P.M. Pardalos, A genetic algorithm for the weight setting problem in OSPF routing. Journal of Combinatorial Optimization 6 (2002), pp. 299–333. Abstract-INSPEC | Abstract-Compendex | $Order Document | Full Text via CrossRef



		This Document


			SummaryPlus
			Full Text + Links
			·Thumbnail Images
			PDF (259 K)



		Actions


			Cited By
			Save as Citation Alert
			E-mail Article
			Export Citation

A tabu search algorithm for the routing and capacity assignment problem in computer networks

Abstract

Article Outline